"Sierpinski" Challenge

Welcome to an exciting challenge regarding fractals!

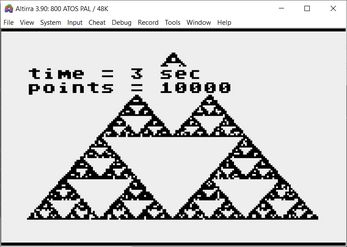
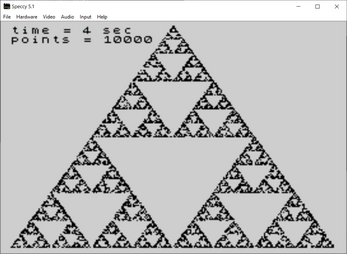
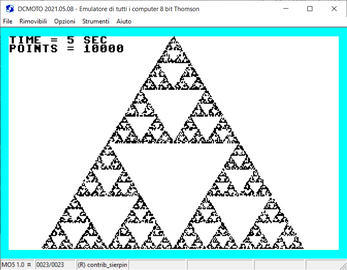
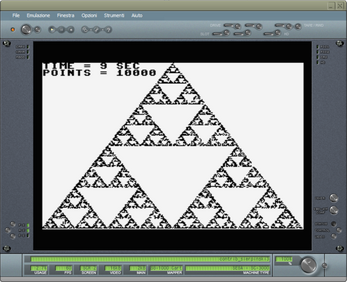
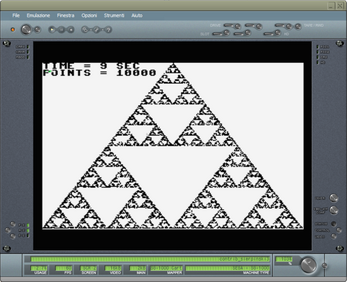
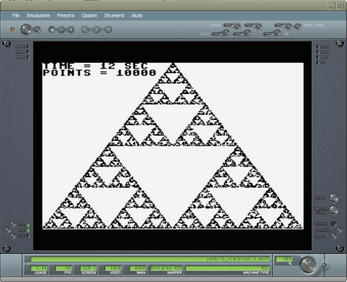
A single source code written in ugBASIC reproduces the famous Sierpinski triangle on many different 8 bit retro computers like ATARI 400/800, Commodore 64, Commodore PLUS/4, ZX Spectrum 48K, Dragon 32/64, Thomson MO6 (standard and U, V, W series), Olivetti Prodest PC128, Thomson MO5 (standard and QW, E, 5E, DE, 5N, 5NR series), MSX, SEGA SC-3000 and SEGA SG-1000. Moreover, it shows on the screen the time  (seconds) needed to draw it with at least 10.000 points.

This source joined the challenge on RetroProgramming Italia - RP Italia.

WHAT IS A SIERPINSKI TRIANGLE?

The Sierpinski triangle is a very simple fractal to obtain. It takes its name from the mathematician who first studied its properties. Such a triangle can have different shapes and sizes and can be obtained in various ways. 

HOW DO YOU CREATE IT?

One of the methods to create it is the so-called Game of chaos: the fractal is built by creating iteratively a sequence of points, starting from a random initial point, in which each point of the sequence is a given fraction of the distance between the previous point and one of the vertices of the polygon; the vertex is chosen at random in each iteration. 

If the first point was a point on the Sierpiński triangle, then all the next points lie on the Sierpinski triangle. If the first point to lie within the perimeter of the triangle is not a point on the Sierpinski triangle, none of the following points will lie on the Sierpinski triangle, but they will converge on the triangle. If the first point is outside the triangle, the only way it will land on the actual triangle, is the next point is on what would be part of the triangle, if the triangle was infinitely large.

It could be difficult to understand... anyway, repeating this iterative process a large number of times, and selecting the vertex at random at each iteration, often (but not always!) it produces a fractal shape. Using a regular triangle and the factor 1/2, it will result in a Sierpinski triangle.

HOW MUCH HAS UGBASIC HELPED?

This cross-platform demonstration would not have been possible without using ugBASIC : it is an isomorphic language and it has cross compilers that works on Linux and Windows, that directly converts high level algorithms into the assembly equivalent for the given CPU / computer.  

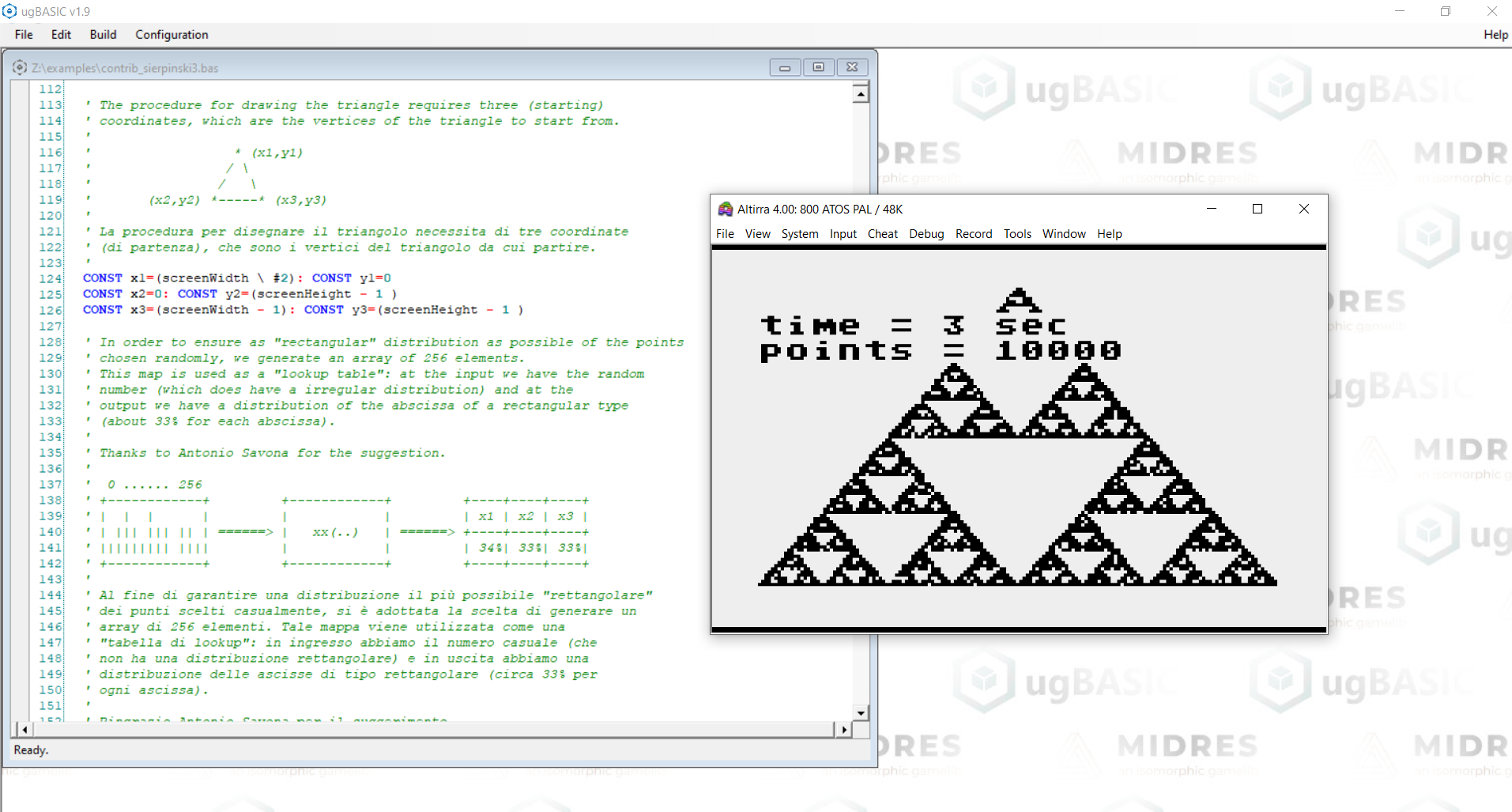
Developing for multiple platforms requires very little effort because the source does not have to be adapted. With a single source code you can obtain programs for multiple retro computers, even very different from each other. Moreover, each target can have a dedicated optimizer, which allows to achieve very interesting results while leaving the BASIC code fully readable. Finally, an useful IDE is also available under Windows.